Wenshan Wang |

王雯珊

STUDY ON TASK PLANNING FOR UBIQUITOUS ROBOTIC SYSTEMS IN COMPLEX ENVIRONMENTS

In ubiquitous robotic systems, sensors and actuators are distributed as modules in the environment, where these modules are able to communicate and cooperate with each other through the network. The ubiquitous robotic technology is able to compensate the insufficiency of artificial intelligence in the development of service robots. It has great advantages including low cost, easy expansion, good reusability, high efficiency and high robustness.

One of the key problems for the ubiquitous robotics is how to coordinate the heterogeneous components in different tasks, in optimization of time and resource consumptions. Compared to the task planning for traditional robotic system, the tasks in ubiquitous robotic system are of higher dimension and with nondeterministic and non-stationary nature.

To address these problems, a new model for task planning is proposed. This model has the expressivity for nondeterministic problems and the efficiency for the high dimensional problems. Based on this new model, an online adapting algorithm for the non-stationary environment is developed, aiming at establishing a ubiquitous robotic system that can adapt and learn. Further, an automated task decomposition method is developed, in order to solve the high dimensional problem. This is achieved by analyzing the variable dependencies. The similar sub-problems could be reused to further improve the efficiency. The task planning methods are tested both in simulation and physical systems.

The main contents of this study are:

1. In order to solve the high dimensional and nondeterministic problems in the ubiquitous robotic system, a Reduce Markov Decision Process (RMDP) model is proposed. This model is able to model the uncertainties of the task, and effectively reduces the branching factor of the state transitions, so that it better represents large-scale problems.
2. In order to improve the planning efficiency, a heuristic initialization method is developed. The RMDP problems are firstly relaxed to a deterministic problem, and then the heuristic functions are utilized to initialize the value function of the states. This method is tested on problems in different sizes with different iteration algorithms. In order to enable the planner to work in non-stationary environment, an online adjustment method is proposed. The probabilities of state transitions are adjusted online according to the execution results from each component.

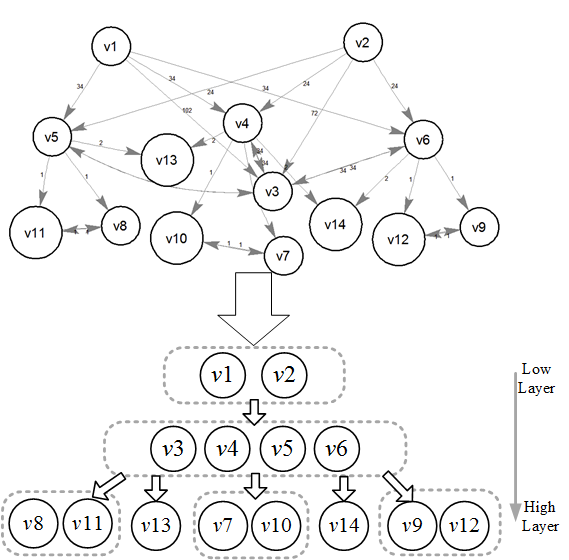
3. A Hierarchical Option Causal Abstraction (HOCA) algorithm is proposed. The main procedures are like this. First, a causal graph is calculated based on the dependency between variables. The state space is divided into topological graph based on the causal graph. Then in each layer, the actions or abstracted options are abstracted into higher-layered options, which induce sub-goals and sub-tasks. At last the sub-tasks and the original task are solved based on semi-MDP theory. Further, the convergence, restricted completeness and optimality of the algorithm are theoretically proved. Experiments are also carried out to validate and compare the algorithms.

   

4. Architecture of ubiquitous robotic system based on component technology is designed and implemented. Based on this framework, two experimental platforms, which are robot bartender task and smart assembly line task are developed. The task planning algorithms discussed in this study are combined and tested in these practical tasks. Detailed analysis and discussions are made based on the experiments. From the theoretical analysis and experimental results, the model and methods proposed in this study can be applied to the ubiquitous robotic task planning problems, and improve the planning efficiency in problems with non-deterministic, non-stationary and high dimensional features.